Photo by Hans-Peter Gauster on Unsplash
Reinforcing Process with Pixar
This past weekend, my family and I purchased tickets to the Science Behind Pixar exhibit that is currently showing at the Denver Museum of Nature & Science. Although I haven't seen a Pixar film in ages, I thought it would be interesting to dig into how these films work under the hood––especially considering that I have no real experience with 3D animation.
Seeing all of the steps that were necessary to bring an idea to a finished product was amazing. It also served as a great, tangible example of how important process is when it comes to solving any complex problem. Per usual––the entire time I was exploring the exhibit, my mind kept turning back to coding and how I could refine my own process, as well as the process of the junior developers I work with every day.
Whether Pixar employees are modeling a character, creating digital rigs, or simulating entire environments––each part of the filmmaking process always followed these four steps:
"Understand, Deconstruct, Implement, Iterate"
This held true across all of the steps in the technical process of making a Pixar film, from beginning (modeling) to end (rendering). This process of solving problems really came to life at the modeling stations, which showcased how characters and objects are made with geometric modeling.

From sketches to digital sculpting, Pixar artists follow a systematic process
For this part of the process, artists spend time understanding a character through the creation of sketches and clay models. Digital modelers then create a virtual 3D model by deconstructing the complex character object into simpler shapes. From there, a digital wireframe is implemented to create the character. Lastly, modelers iterate on the wireframe via digital sculpting and smoothing.
Seeing this in action reinforced my belief that making headway (and finding success) while solving problems requires a process. Utilizing these four-steps translates very well when solving programming problems––as evidenced both from my own experience as well as what I've witnessed from teaching others.
Yesterday morning, my teammate and I distributed a timed challenge for our junior developers to work through. At a quick glance, this particular code challenge might seem insurmountable. However––when one follows a well-defined process, this is not the case. Discovering and utilizing a process takes time, practice, and refinement––but doing so is definitely well within anyone's reach.
Since I had never done this challenge myself, I decided to work through it on my own and write about how I approached it. I should note that the process of understanding, deconstructing, implementing, and iterating is not perfectly linear. As I approached each part of the process, I generally found myself straddling the line between 1 of 2 steps… or pushing myself back several steps (iteration) when something wasn't working. However––it was following this process of steps that helped guide me towards a successful solution.
Here's how I put this process into action:
The Problem
TASK: Write a program that checks if a Sudoku board is completed correctly. The input of the board will be provided in an array matrix (example below). Your output should be a boolean.
var input = [
[4, 3, 5], [2, 6, 9], [7, 8, 1],
[6, 8, 2], [5, 7, 1], [4, 9, 3],
[1, 9, 7], [8, 3, 4], [5, 6, 2],
[8, 2, 6], [1, 9, 5], [3, 4, 7],
[3, 7, 4], [6, 8, 2], [9, 1, 5],
[9, 5, 1], [7, 4, 3], [6, 2, 8],
[5, 1, 9], [3, 2, 6], [8, 7, 4],
[2, 4, 8], [9, 5, 7], [1, 3, 6],
[7, 6, 3], [4, 1, 8], [2, 5, 9]
]
isValidSudoku(input); #=> true
var input = [
[4, 3, 5], [2, 6, 9], [7, 8, 1],
[6, 8, 2], [5, 7, 1], [4, 9, 3],
[1, 9, 7], [8, 3, 4], [5, 6, 2],
[8, 2, 6], [1, 9, 5], [3, 4, 7],
[3, 7, 4], [6, 8, 7], [9, 1, 5],
[9, 5, 1], [7, 4, 3], [6, 2, 8],
[5, 1, 9], [3, 2, 6], [8, 7, 4],
[2, 4, 8], [9, 5, 7], [1, 3, 6],
[7, 6, 3], [4, 1, 8], [2, 5, 9]
]Understand
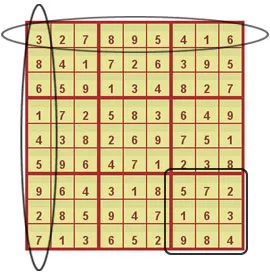
Since I've never played Sudoku, I wasn't entirely sure of the rules of the game. Given this, I spent a good 5 - 7 minutes reading through this article to feel confident that I even understood the problem in the first place. If you aren't familiar with Sudoku, I would encourage you to read through the article linked above before going any further.
45 is the magic number
Based on the rules of the game, I decided very early on that I needed to add all of the numbers in each row, column, and square and then check each sum against the value of 45 (which is the sum of numbers 1 – 9). Knowing this, I immediately planned to separate functionality as such: find a sum, gather values for a row, gather values for a column, and gather values for a square.
Next, I looked for patterns in the input examples. Here are some of the things that I noticed:
Every 3 sub-arrays made one row
Ex: Row 1 => subArray0, subArray1, subArray2

3 subArrays in a row
All values in a column shared the same index and were aligned by every third sub-array
"Ex: Column 1 => subArray0[0], subArray3[0] … subArray18[0], subArray21[0], subArray24[0]"

Every third subArray with a shared index
A square consisted of three sub-arrays that were made up of every third sub-array
Ex: Square 1 => subArray0, subArray3, subArray6

Every third subArray to total three arrays
Much of this part of my process was spent thinking aloud, diagramming, and discovering/labeling the patterns I found in the example inputs.
Deconstruct and Implement
For the next part of my process, I started to deconstruct the larger problem based on what I knew from the patterns that were discovered earlier.
Sum
The first piece to deconstruct? Any row, square, or column's sum should be 45 to be valid. If this was not true at any point in the process, the Sudoku board was invalid. I originally intended for this helper function to only check the sum of each row. Because of this, my function definition took in the three sub-arrays that were needed to reduce to the row's sum:
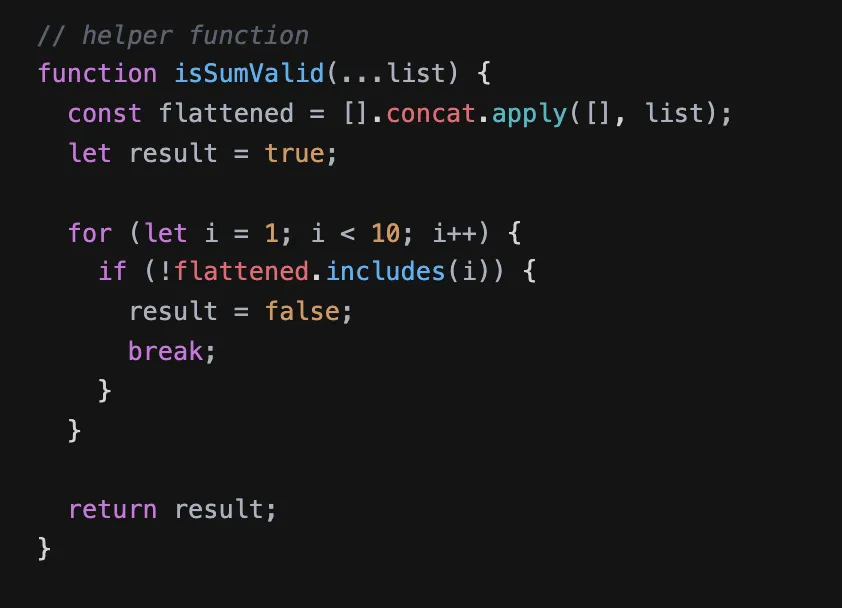
First piece of code to implement: isSumValid
I tested this piece of functionality by using a variation of mocked inputs to analyze my expected vs actual output. This was the first piece of code that I implemented.
Row
From here, the next piece to deconstruct was the functionality for checking a row's validity. To do this, I decided I would iterate over the original list and pass sub-arrays in groups of 3 to isSumValid. To have easy access to the original parameter, I scoped this logic within the main function. I also planned to use conditional logic to keep track of whether isSumValid returned true or false. In the event that isSumValid did verify a row as false, the loop would end immediately since one false flag confirmed the board's invalidity. If we made it through all of the rows without any values of false being returned, then we could be certain that all rows were valid.
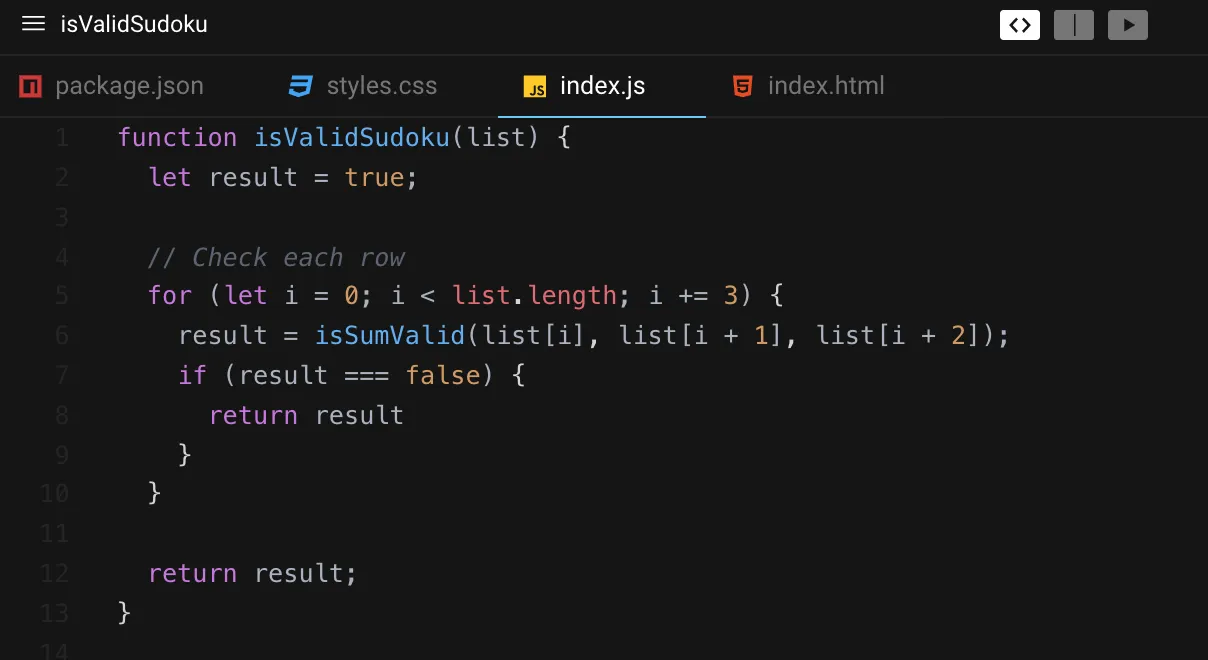
Checking for the validity of each row
After testing this piece of functionality in isolation, I moved on to deconstructing the functionality for checking columns.
Column
From the start, my plan was to iterate over the original parameter (again) to grab the values from each column. After revisiting my diagrams/drawings, I kept coming back to the approach of grabbing the "top" of every column on each iteration. Since I was trying to avoid creating multiple arrays (to hold the values from each of the 9 columns), I stretched my brain to come up with a way where I could add each value from each column, in real-time. After some thought and pseudo coding, I landed on the path of creating a closure that would keep track of adding values together… with logic in place so that the final result would only be returned once 9 values were given.
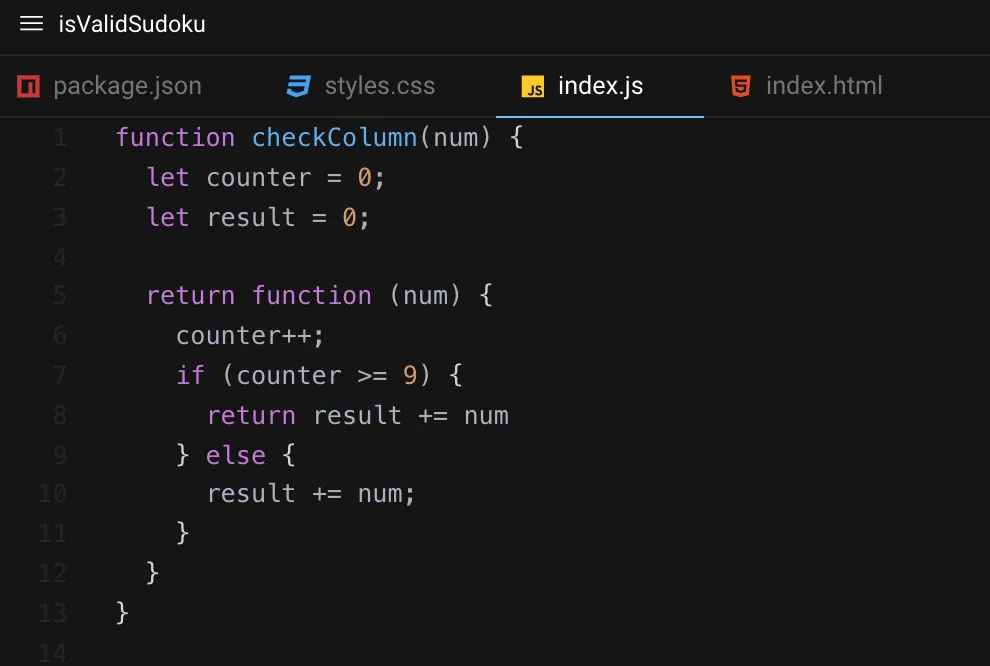
Closures are fun
Once the final result of each column was returned, I would save each number to an object literal that tracked my columns. To keep track of the 9 results for each column, I needed to create 9 scopes to track the 9 columns:
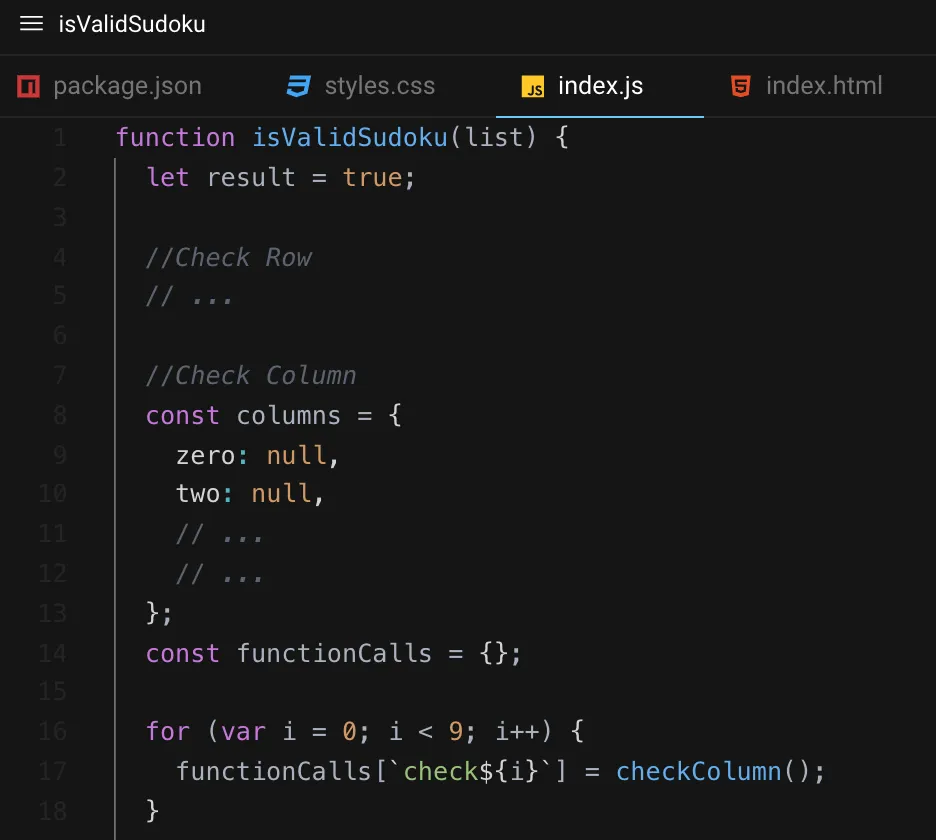
Adding values from a column: Part I
Once the final result for each column was returned, I would be able to iterate over the values in my column object to verify that the sums were all 45.
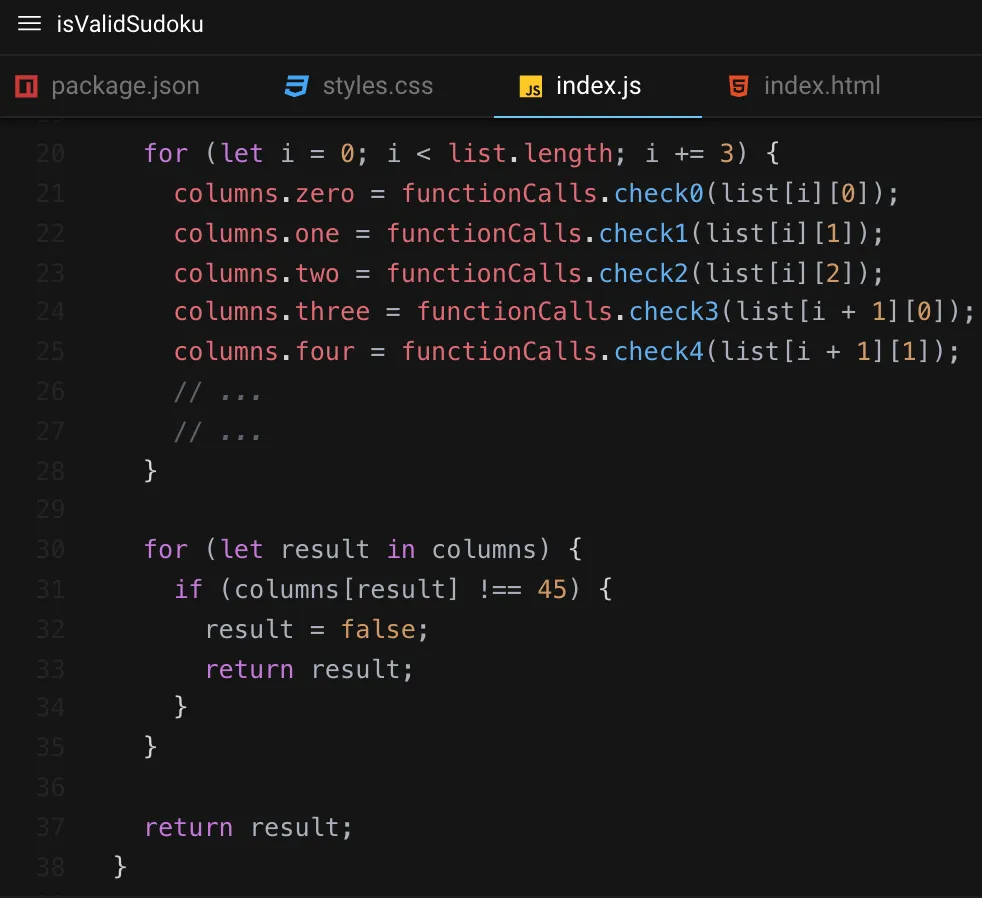
Adding values from a column: Part II
As I was thoughts this piece of functionality, I became more and more certain that I would end up iterating on my implementation. First, I was not a fan of having duplicated logic for checking the sum since I had already defined a function to do just that. Secondly, I wasn't fond of the number of scopes that I needed to create/track to make this particular approach work. Lastly––the use of closures to protect the final result of each column felt like it was a bit much for this problem (in hindsight, it was).
However––since this was administered to our devs as a timed challenge, I approached solving it with the idea that I, too, had similar time constraints. Because of this, I kept what I had (which was working) and made a plan to come back to this code once I got the last third of my functionality done. I figured that I must have missed other patterns along the way and that solving the last bit of functionality might shed some light on those missing pieces. After testing this piece of functionality in isolation, I moved on to the squares.
Square
The last portion to deconstruct was finding the sum of all numbers in every square. Since I knew that a square consisted of 3 sub-arrays made up of every third array, I originally wrote logic to handle the first "row" of squares:
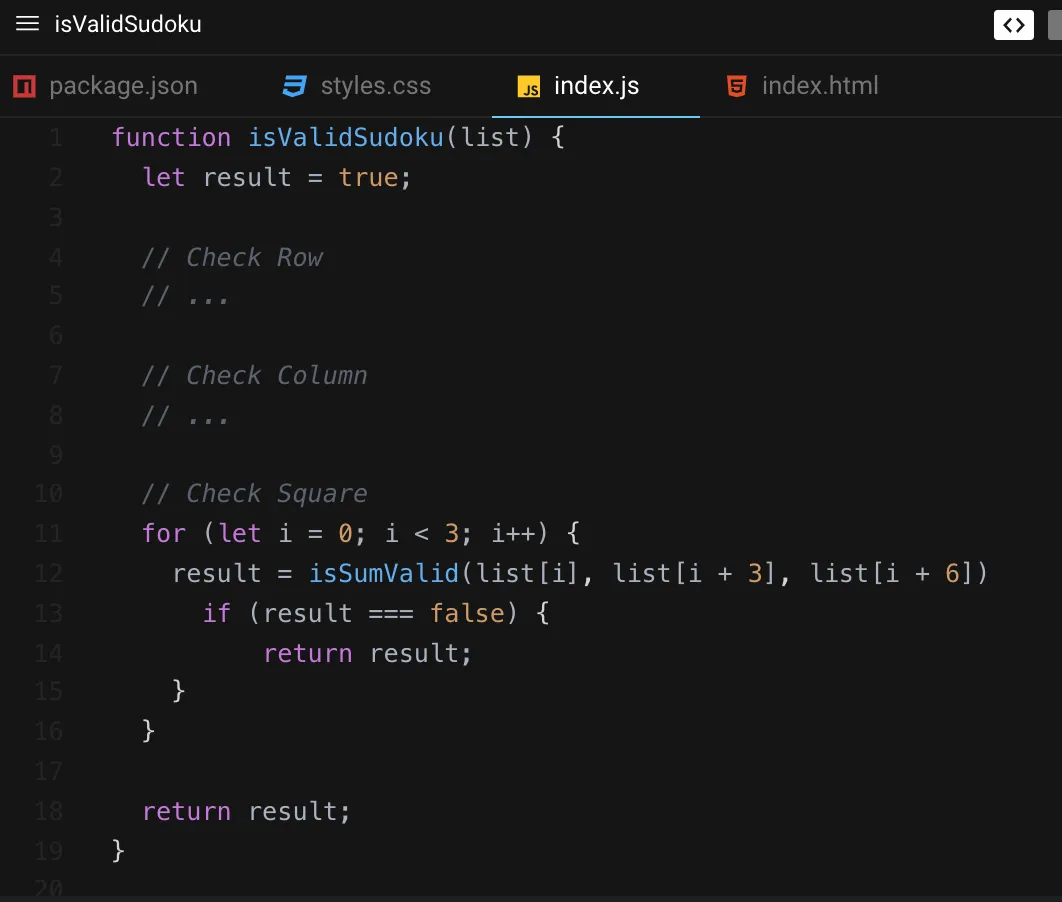
This could lead to 3 nearly identical loops…😬
From here, I saw that I would need to modify i to account for the "top" or start of the next row of squares, at subArray9, subArray10, and subArray11. I would then have to repeat this process for subArray18, subArray19, and subArray20. Rather than set up three separate loops, I opted to utilize conditional logic to reset my i variable once a "row" of squares had been validated:
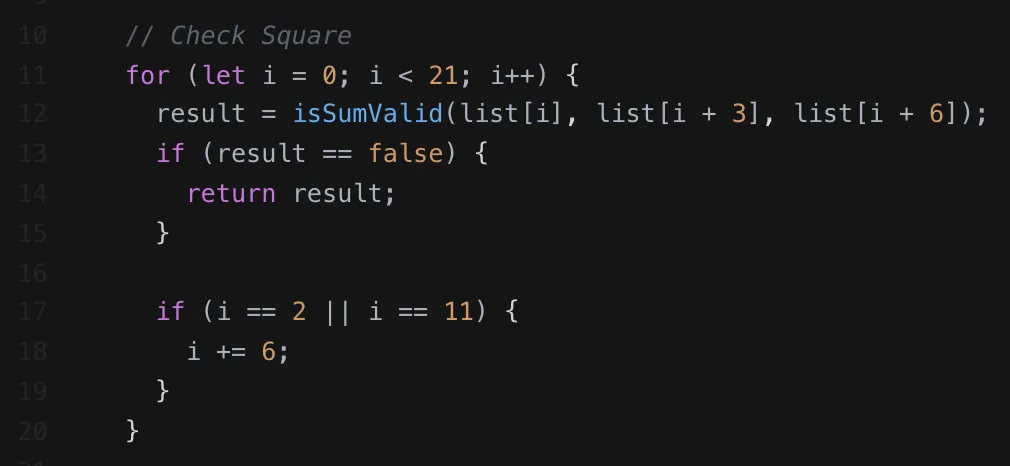
That's better.
After refactoring for duplication and testing the functionality in isolation, I felt confident that I could revisit my implementation of tracking columns.
Iterate
Column: Take Two
As I mentioned earlier, the process of understanding, deconstructing, implementing and iterating is certainly not linear. The biggest proof of this comes from my eventual return to this part of my code.
After reviewing the way I approached finding the sum for the rows and squares-—I wanted to find a way to utilize the isSumValid helper function for each column. I did not want to implement nine closures… and I certainly did not want to wait until all of the sums were generated for all 9 columns before verifying whether any one column was valid. Ideally, my logic would add the values of each column and then immediately check the sum. Similar to the logic that I used in the other pieces of functionality––I did not want to check any extra columns after one was determined to be invalid.
This led me to implement functionality that would grab all the values from one column by placing three numbers at a time in an array. Once the 3 arrays were filled, the isSumValid function would be utilized to flag the column's validity. If the column was invalid, the iteration would end and the entire board would be invalidated. If the column was valid, the process would continue with the next column. The implementation can be found below:
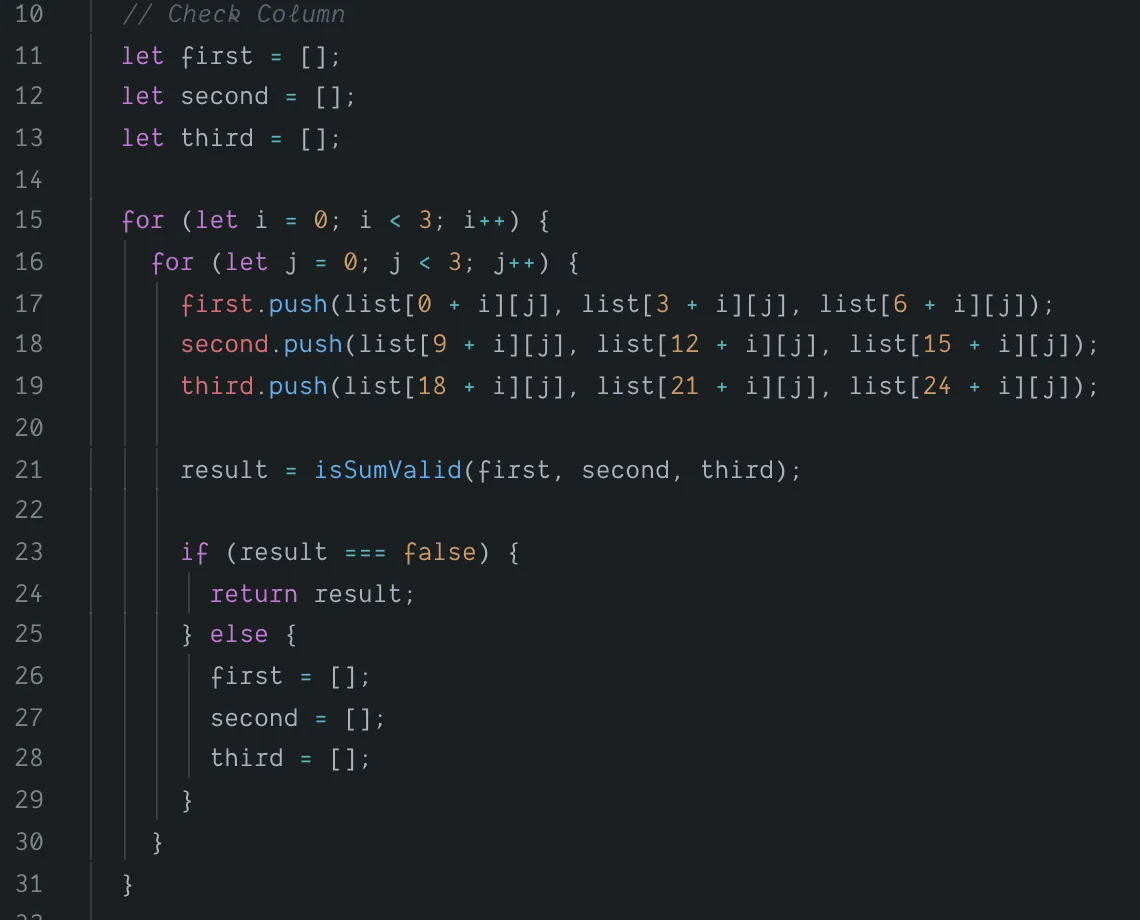
Making use of isSumValid to check columns
Although I wasn't thrilled about using hardcoded values for the index of columns, I felt much better with this alternative way of adding the values for columns. Similar to the pieces of functionality that came before it, I thoroughly tested this piece of logic in isolation before finalizing it.
Process is Key
By following this 4 step problem-solving process, I was able to arrive at a solution to the original prompt. I may not know 3D animation like the folks at Pixar… but I've solved enough problems to know that process is key when it comes to solving anything complex.
The final solution (with refactoring for edge cases) can be found at the bottom of the post.
Update
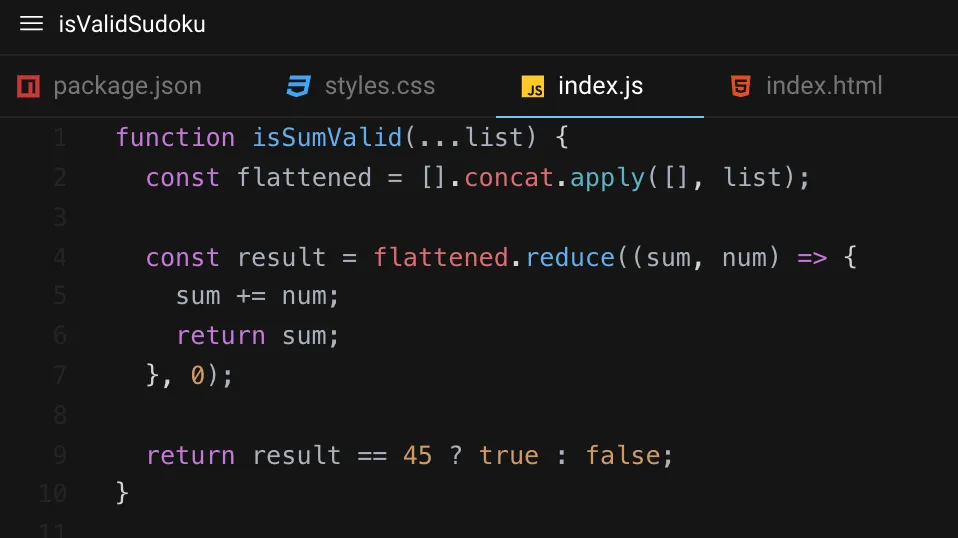
The original solution from this timed challenge did not account for a sudoku board that does have rows/columns/squares that sum to 45> but does not have each unique number from 1 – 9 (ex: the entire board is filled with 5s). To account for this, isSumValid should be refactored: